Elliptic Curve Cryptography - A Primer
Cryptography is arguably one of the largest talking points in the tech space, by varied audiences at that - chat users, spy agencies, governments, tech companies, and of course, researchers. Prof. Dan Boneh’s amazing Cryptography I had given me a good primer on crypto systems, and to keep myself updated with the algorithms of today, I dove into the world of today’s crypto - at least some shallow backwaters of it. Most of the topics I ended up reading on were influenced by either my past reading or hearing about them from the people around me - thus not a complete or state-of-the-art list - but just a few ones which I found cool and are usually not covered in textbooks. I’ll be covering a few of these in the coming weeks. To start with, let’s look at elliptic curve cryptography.
Let’s cover our basics first. Cryptography today is inherently based on the principal that math is hard, or find math that’s so long or so hard that even computers cannot solve it without taking billions of years (even if you give half the population a few hundreds of the most cutting-edge parallel processing machines - 3brown1blue has a great short video on this complexity). The notion here is that we take our plaintext, do a lot of mathematical processing to it, maybe do this multiple times, and then hopefully, it looks like a random string of characters. The aim of cryptogrpahy algorithms is to leak as little information as possible, including how patterns in plaintext should not be revealed in ciphertext, or how modifying something that the attacker controls cannot blindly modify the resulting plaintext after decryption (we aren’t talking about integrity yet!). To aid this randomization, one or more keys are used. Symmetric cryptography uses the same key for encryption and decryption, and asymmetric crypto algorithms use a different one for encryption and decryption. The secure distribution of symmetric crypto keys led to research in key-exchange, and powerful algorithms in asymmetric crypto and key derivation came to the fore.
The keys that we talked about before, or generally, the constants involved in the encryption and decryption process, are usually large prime numbers. The RSA algorithm for example, relies on the difficulty of factorizing a product of two large prime numbers, while the Diffie-Hellman Key Exchange algorithm relies on the difficulty of finding a logarithm of a given number to a publicly-known base efficiently, if the numbers are sufficiently large. We call these as the trapdoor functions - functions that enable you to go from A to B easily (A -> B), but won’t let you go from B to A (A <-x- B) easily.
We’ll come back to this complexity problem at the end.
Elliptic Curve Cryptography
We mentioned RSA before, and the fact that it relies on prime factorization as a difficult problem for its security. We also mentioned the discrete log problem in Diffie-Hellman. Elliptic Curve Cryptography (ECC) uses a combination of these as its trapdoor function.
First up, what is ECC? ECC is another public-key cryptosystem which uses elliptic curves as its base. An elliptic curve is a curve in the x-y plane which follows the following equation:
$$ y^2 = x^3 + a*x + b $$
Specifically for ECC, we restrict the size of the coordinate system as a finite-field, restricting how far the curve can go in either directions. One good example of an elliptic curve can be seen in the below figure (this image is one part of a larger image taken from the Wikimedia Commons)
An example ECC curve with an addition line through it
Specifically for ECC, we use our parameters a and b to define a curve such that a line through any two points on the curve always intersects the curve at a third point in our finite field (and we make use of modular arithmetic for this). Also, the curve itself is symmetric about the X-axis. There are certain peculiarities about addition and multiplication of numbers along this curve that aid in ECC.
Now, looking at the example line given in the figure above, we see that the line in the figure is P + Q + R = 0, i.e. P + Q = -R, i.e. R can be interpolated in the -Y direction to get our sum (given that the curve is symmetrical). Now, adding P to R would yield us another number along the curve, which can be then extrapolated about the X-axis to give us a new result. If this addition is done of a point with itself, n times, it would effectively mean multiplication of the point by n, at the end of which, we’ll get another number on the same curve. The GIF below succintly summarizes this addition operation (credits to Cloudflare).
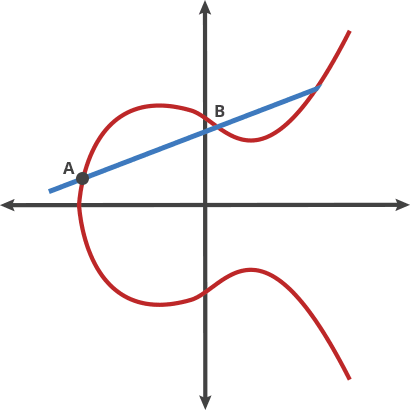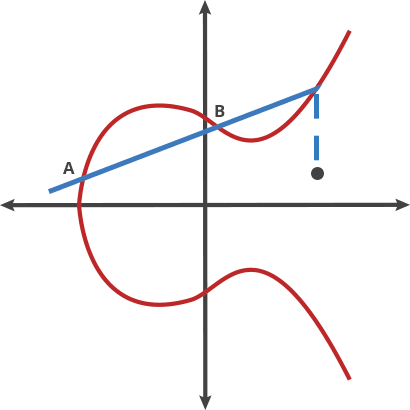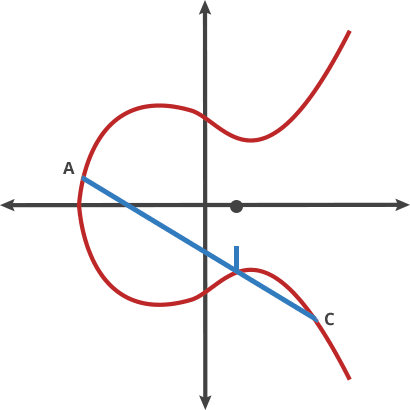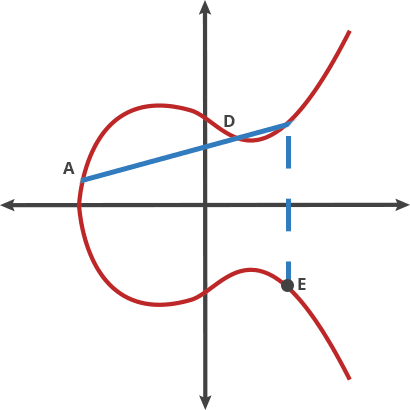
An example of addition on an ECC curve.
The trapdoor property that ECC exploits here is the elliptic curve discrete log problem, which basically is that given the result of the aforementioned multiplication, it is difficult to find the number ’n’ with which the original point was multiplied, i.e. given two points P and Q on the curve, if nP = Q, it is difficult to compute n.
Keys in ECC
ECC generally uses one of the standard defined curves. Each curve will have a publicly known “generator point” G, on the curve.
We pick a random number “k” as our private key. The public key then becomes Q = k * G. Thus, the difficult problem now comes to compute the private key given the public key and the publicly-known generator.
What can be done with these two is an implementation detail. A secret-sharing algorithm using this key-pair, called the ECDH (Elliptic Curve Diffie Hellman) is common, following which, the shared secret is used for symmetric cryptography. Elliptic curves are also used for digital signature algorithms (ECDSA and EdDSA).
Why the hype?
ECC are advantageous over RSA mainly in terms of key size, while RSA wins in terms of computational complexity. But the gains for ECC in terms of key size are large - a 256-bit ECC key would give the same security as a 3072-bit RSA key, which is a large gain.
Some standard curves and where ECC is used today
Curve448 (equation 1) and Curve25519 (equation 2) are the most commonly used elliptic curves today.
$$ \tag{1} y^2 + x^2 = 1 - 39081 * x^2 * y^2 $$ $$ \tag{2} y^2 = x^3 + 48662 * x^2 + x $$
Both of these are the standard supported curves for TLS v1.3. Curve25519 has had a lot of other applications too, including DKIM, Signal Protocol, SSH, Matrix Protocol, Wireguard, etc.
Interesting sidenote - Dual_EC_DRBG
Dual Elliptic Curve Deterministic Random Bit Generator (Dual_EC_DRBG) was a psuedo random number generator, which was standardized by NIST in 2006. The PRNG used elliptic curve principles to generate random numbers. There was a backdoor in the algorithm though, and it allowed the designers of the algorithm parameters to predict the next numbers generated. Interestingly enough, NSA had pushed for Dual_EC_DRBG and had designed the parameters for standardization, leading to suspicions that the backdoored PRNG was being shoved in major libraries and devices (see RSA BSAFE and Cisco - NSA Bullrun program). Computerphile has an excellent video on this backdoor.
While we talked about hard problems and trapdoor functions, we should remind ourselves that the security of all of these are purely dependent on the computational complexity of the math behind these problems. With the rise in quantum computers, seemingly difficult problems are becoming extremely easy to solve, and these quantum computers are therefore, a big threat towards the security of the crypto algorithms we have in place today. To counter this, a whole new suite of algorithms are now being adopted, under the umbrella of post-quantum cryptography. We’ll take a look at few of these soon.